Maximum Depth of Binary Tree
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
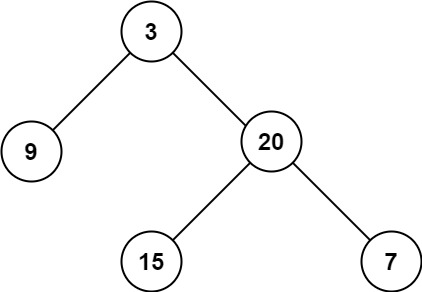
Input: root = [3,9,20,null,null,15,7] Output: 3
Example 2:
Input: root = [1,null,2] Output: 2
Example 3:
Input: root = [] Output: 0
Example 4:
Input: root = [0] Output: 1
Constraints:
-
The number of nodes in the tree is in the range
[0, 104]. -
-100 <= Node.val <= 100
Solution 1:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right)
{
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}
else{
int left = maxDepth(root.left);
int right = maxDepth(root.right);
if(left > right)
return left+1;
else
return right+1;
}
}
}
Here, we are going to find depth of the binary tree using recursion.
1) If root is null, then return 0.
2) Else,
a) Find maxDepth of left subtree (recursively)
b) Find maxDepth of right subtree (recursively)
c) Then, if left greater than right tree, then, left + 1, else right +1.
Now, you understand the logic behind this problem.
Want to reduce a big code to small lines of code? Check below solution.
Solution 2:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right)
{
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
int leftheight=maxDepth(root.left);
int rightheight=maxDepth(root.right);
return Math.max(leftheight,rightheight)+1;
}
}
The above solution is exactly same as solution 1. Instead of doing if
else to find which tree is having maximum depth, here we are using
Math.max(). Remaining all logic are same as solution 1.
Comments
Post a Comment