Longest Common Subsequence
Given two strings
A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, "ace" is a subsequence of "abcde" while "aec" is not). A common subsequence of two strings is a subsequence that is common to both strings.
If there is no common subsequence, return 0.
Example 1:
Constraints:
Try it on Leetcode
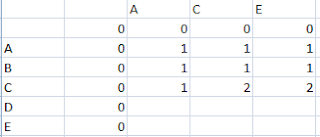
Here the above solution is solved based on hints given in this page. Click here and see HINT 2 at bottom of description. It is easier to understand when you learn these type of solution with table. Please draw the table and update table based on above algorithm then you will understand much faster.
Here we are providing description based on the example 1.
Now take example text1 = "abcde", text2 = "ace"
1) Then these two strings are converted into char array and creating a table with size of m+1 and n+1, where m is length of text1, n is length of text2.
2) Initially first row and first column are 0 by default.
3) If character belongs to corresponding row and column are equal[i.e., i-1 & j-1], then update current cell as 1.
3) Else update the cell with maximum of previous row element and previous column value.
4) Repeat step 2 and step 3 until, it reaches last cell of table.
5) Last cell i.e., lcs[m][n] value represents the common longest subsequence.
Please let us know your views in comment section.
text1 and text2, return the length of their longest common subsequence.A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, "ace" is a subsequence of "abcde" while "aec" is not). A common subsequence of two strings is a subsequence that is common to both strings.
If there is no common subsequence, return 0.
Example 1:
Input: text1 = "abcde", text2 = "ace" Output: 3 Explanation: The longest common subsequence is "ace" and its length is 3.Example 2:
Input: text1 = "abc", text2 = "abc" Output: 3 Explanation: The longest common subsequence is "abc" and its length is 3.Example 3:
Input: text1 = "abc", text2 = "def" Output: 0 Explanation: There is no such common subsequence, so the result is 0.
Constraints:
1 <= text1.length <= 10001 <= text2.length <= 1000- The input strings consist of lowercase English characters only.
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
if(text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0)
return 0;
char[] chr1 = text1.toCharArray();
char[] chr2 = text2.toCharArray();
int m = text1.length();
int n = text2.length();
int i, j;
int[][] lcs = new int[m + 1][n + 1];
for(i = 1; i <= m; i++){
for(j = 1; j <= n; j++){
if(chr1[i - 1] == chr2[j - 1]){
lcs[i][j] = 1 + lcs[i - 1][j - 1];
}else{
lcs[i][j] = Math.max(lcs[i - 1][j], lcs[i][j - 1]);
}
}
}
return lcs[m][n];
}
}
Try it on Leetcode
Here the above solution is solved based on hints given in this page. Click here and see HINT 2 at bottom of description. It is easier to understand when you learn these type of solution with table. Please draw the table and update table based on above algorithm then you will understand much faster.
Here we are providing description based on the example 1.
Now take example text1 = "abcde", text2 = "ace"
1) Then these two strings are converted into char array and creating a table with size of m+1 and n+1, where m is length of text1, n is length of text2.
2) Initially first row and first column are 0 by default.
3) If character belongs to corresponding row and column are equal[i.e., i-1 & j-1], then update current cell as 1.
4) Repeat step 2 and step 3 until, it reaches last cell of table.
5) Last cell i.e., lcs[m][n] value represents the common longest subsequence.
Please let us know your views in comment section.






Comments
Post a Comment